10分で分かる金融工学入門 – 初心者にも分かりやすく解説

金融工学は複雑な数式が非常に多く、挫折した方も多いのではないでしょうか？

しかし、実はその数式の意味を捉えれば誰でも簡単に理解できます。

この記事では、金融工学にはつきものな複雑な用語を丁寧に解説しながら、難解な数式についても丁寧に解説します。金融工学とは何かを理解できるはずです。

金融工学とは何か？

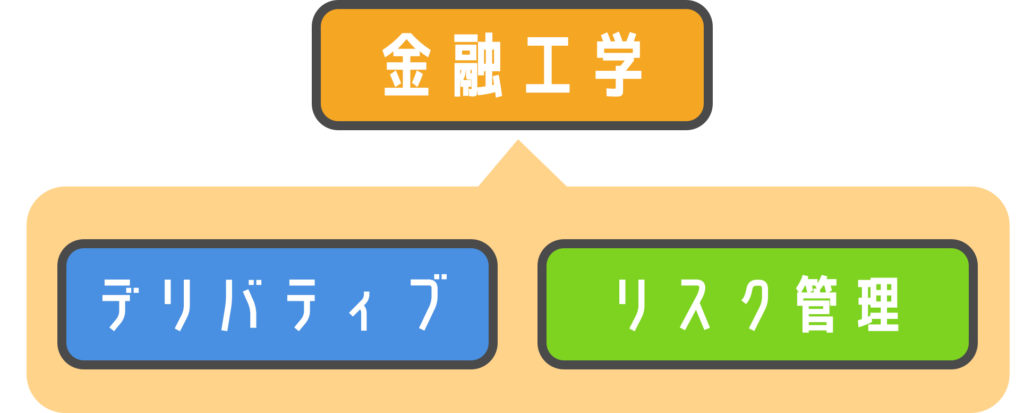
金融工学（Financial Engneering）とは、デリバティブとリスク管理について、数学的に体系化された理論です。日本の記事では、より包括的な学問のように紹介されているものも多いですが、実はこの２つだけなんです。

ファイナンスという学問分野も存在しますが、そのファイナンスの一部分が「金融工学」だと思ってください。つまり、非常に狭い領域の理論です。

複雑な数式を読み解くうちに、「金融工学って何だっけ？」と目的を見失わないように注意が必要です。繰り返しますがデリバティブとリスク管理についての理論です。

デリバティブとは何か？

金融工学は、デリバティブとリスク管理についての理論だとわかりました。ではその１つ目のデリバティブとは何でしょうか？

デリバティブは、日本語では金融派生商品と言います。何から派生した商品なのかというと、株式や債権から派生した商品です。株式や債権のことを金融の世界では原資産といいますが、この原資産から作られた新たな商品がデリバティブです。

株式や債権市場に比べたらデリバティブなんて研究に値するのか？と考える方も多いかと思いますが、実はデリバティブは金融商品の中で市場規模が圧倒的です。

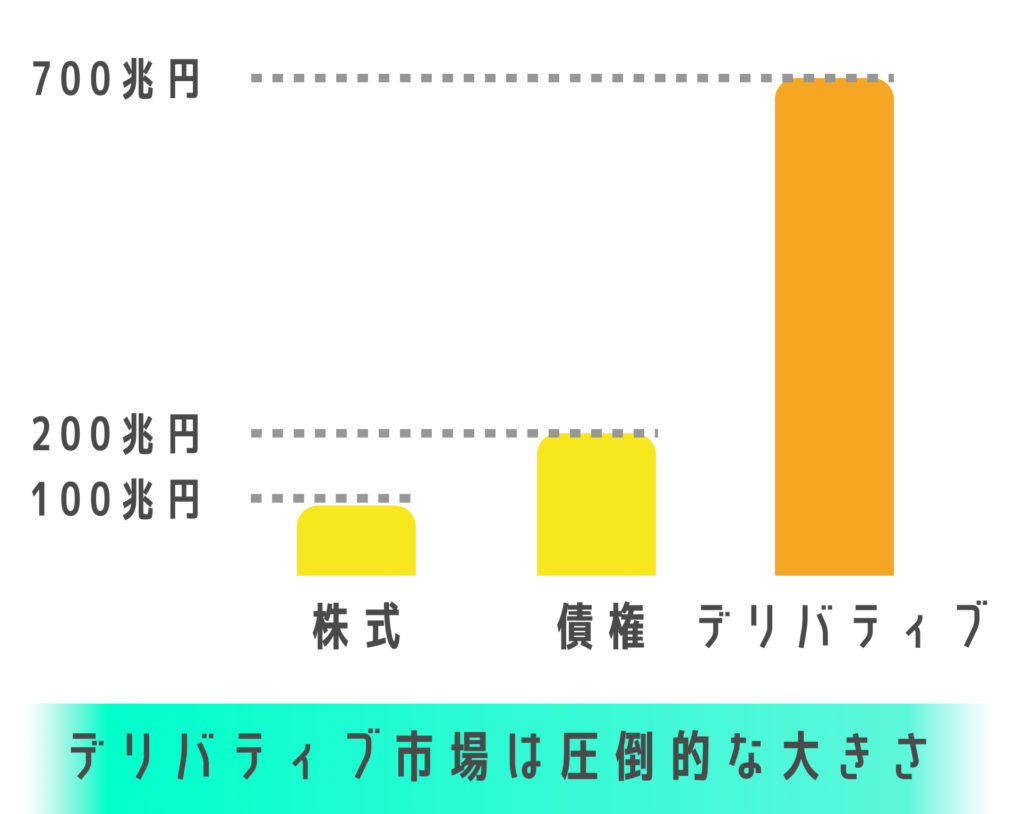
これだけ「原資産」から様々な商品が作られて販売されているということです。これだけ市場が大きいのは金融工学の成果と言えるんですね。

デリバティブの代表例

では、デリバティブとは何かを理解したところで、代表的な商品について紹介していきます。

先物取引

先物取引とは、将来受け渡しする株や債券を現在売買することです。例えばトヨタ株を「1年後に」100株1万円で買うという取引をします。契約に近いですね。

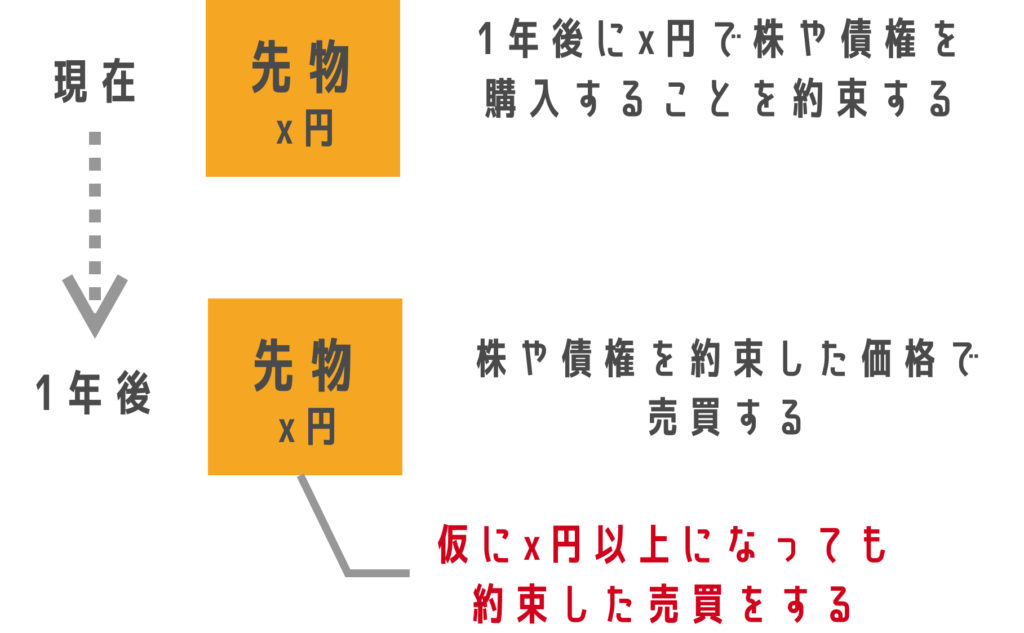
先物は様々な分野に応用されており、原油先物や穀物の先物、為替先物など多数存在します。

オプション取引

オプション取引は将来のある地点での買う権利、売る権利を売買することです。

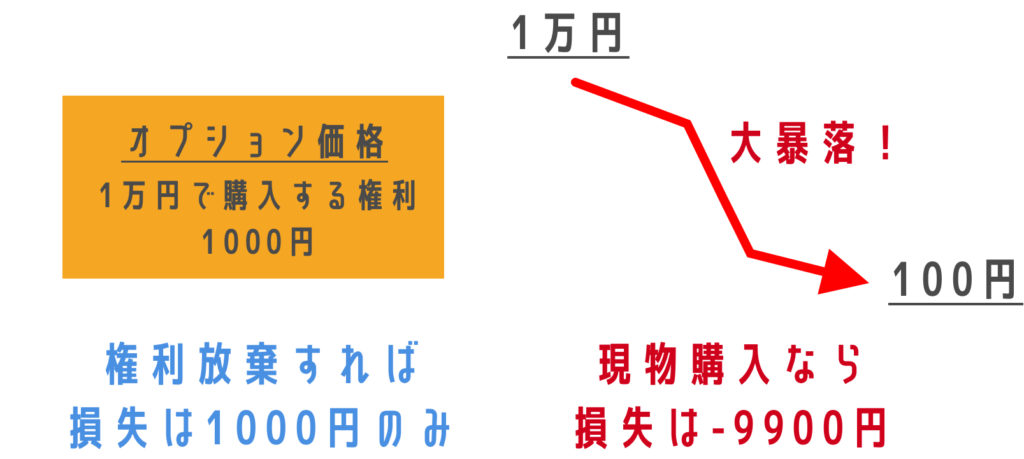
例えば「トヨタ株を1年後に1万円で買うオプション」を購入したとして、仮にトヨタ株が1年後に11,000円になっていれば1,000円の利益を得られます。逆に9,000円に値下がりした場合は、この購入する権利を放棄することができます。

下落したら権利を放棄できるなんて、夢のような取引に見えるかもしれませんが、実際にはオプションには価格がついています。つまり、オプションを購入するにはコストがかかりますから、権利を放棄すると同時にこのコストが無駄になるということです。

オプションの最大のメリットはリスクが事前に分かっていることです。どんなに株価が値下がりしても、最大の損失はオプションの購入価格分となるからです。リスクを嫌う機関投資家にとっては非常に魅力ある商品です。

スワップ取引

スワップ取引とは、デリバティブ同士を交換する取引です。最も活発に取引されているのが「金利スワップ」です。住宅ローンなどでも固定金利と変動金利という２つの金利がありますよね。

固定金利は数年間金利が固定されており、変動金利は毎月変動します。これら２つの商品が活発に交換取引されています。

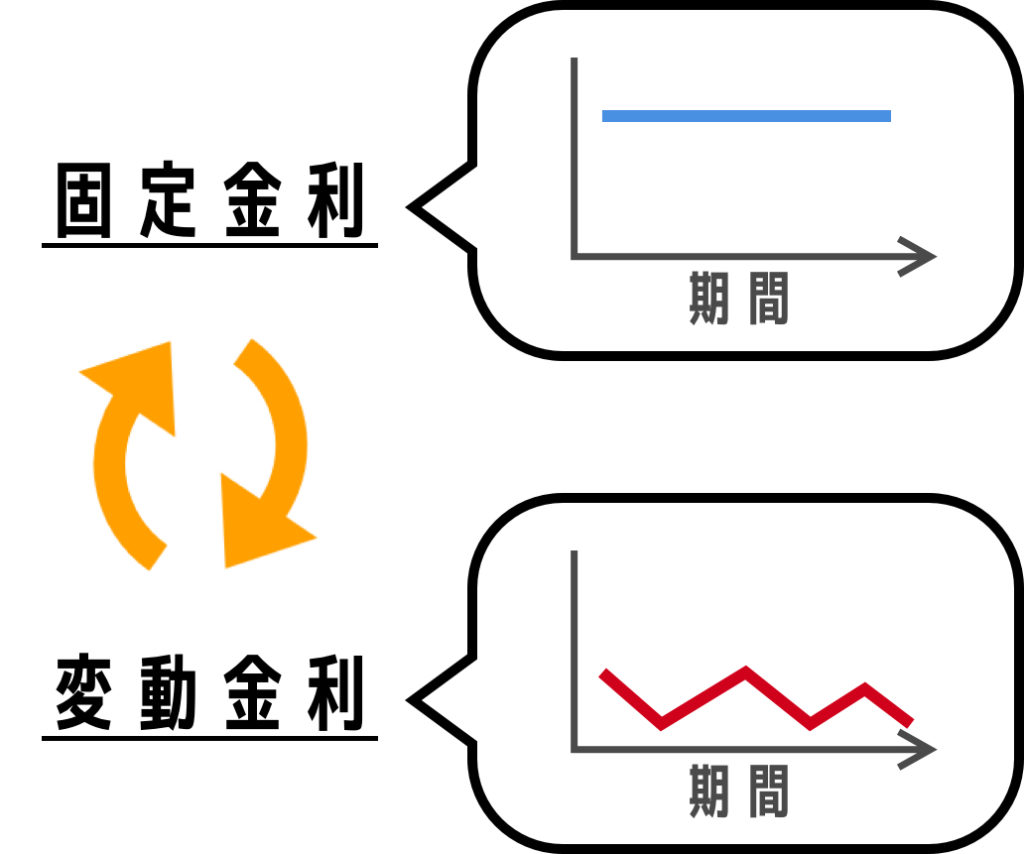
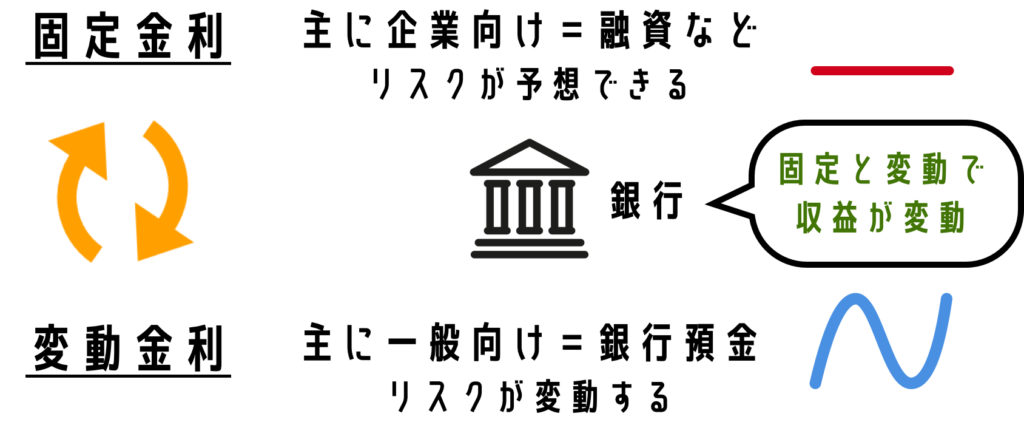
なぜ？と思う方もいるかと思いますが、銀行の多くは一般企業に対して固定金利でお金を融資しています。一方で個人の預金は変動金利です。銀行は固定金利と変動金利の狭間で利益が増減するわけですから、固定と変動を適宜交換することによってリスクを抑えています。

リスク管理

金融工学のもう１つの柱が「リスク管理」です。リスクのみを研究するのか？と思われる方もいるかと思いますが、リスクとリターンについての理論です。

投資の世界ではリスクに対してリターンは相関関係であると考えます。小さなリスクで大きなリターンというものは基本的にはありません。

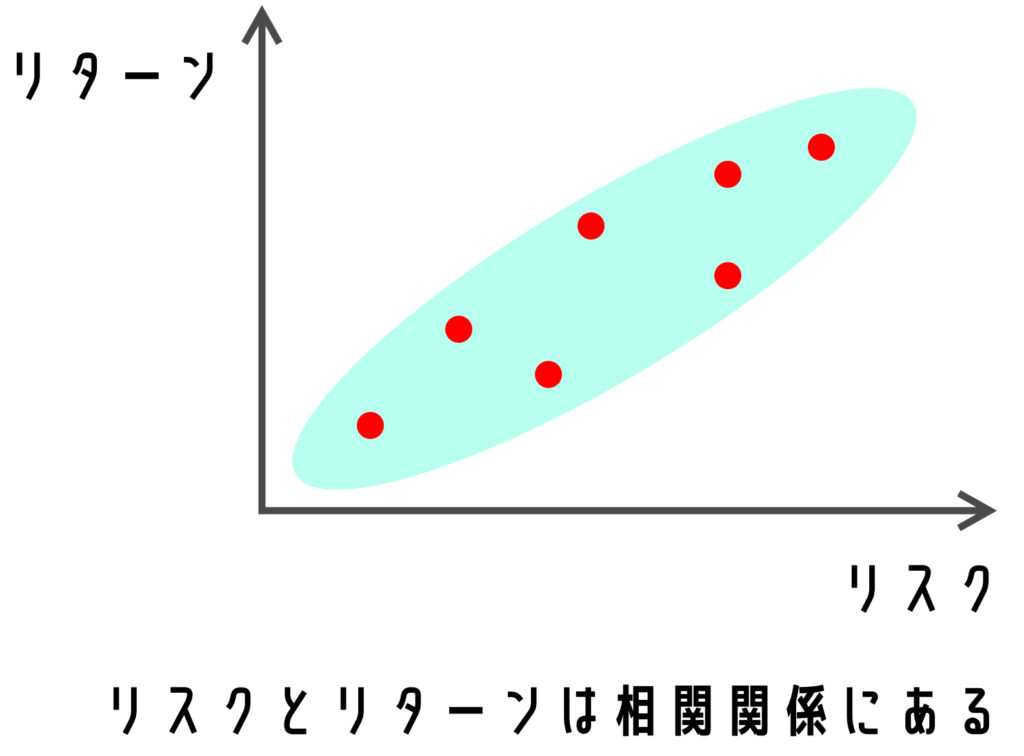
また、金融工学では予想は不可能であると考えます。カリスマ投資家が予想できるというのも所詮デタラメです。

金融工学におけるリスク管理は、リスクの大きさを適切に計算するにはどうしたら良いかを体系的にまとめています。

実はこのリスク管理はデリバティブ商品を作るのに大いに役立ちます。詳しくは次の項で解説しますが、リスクの大きさを正しく図れれば、限りなくリスクを抑えた商品を作ることができますし、同程度のリスクを持つ商品同士を交換することだってできます。

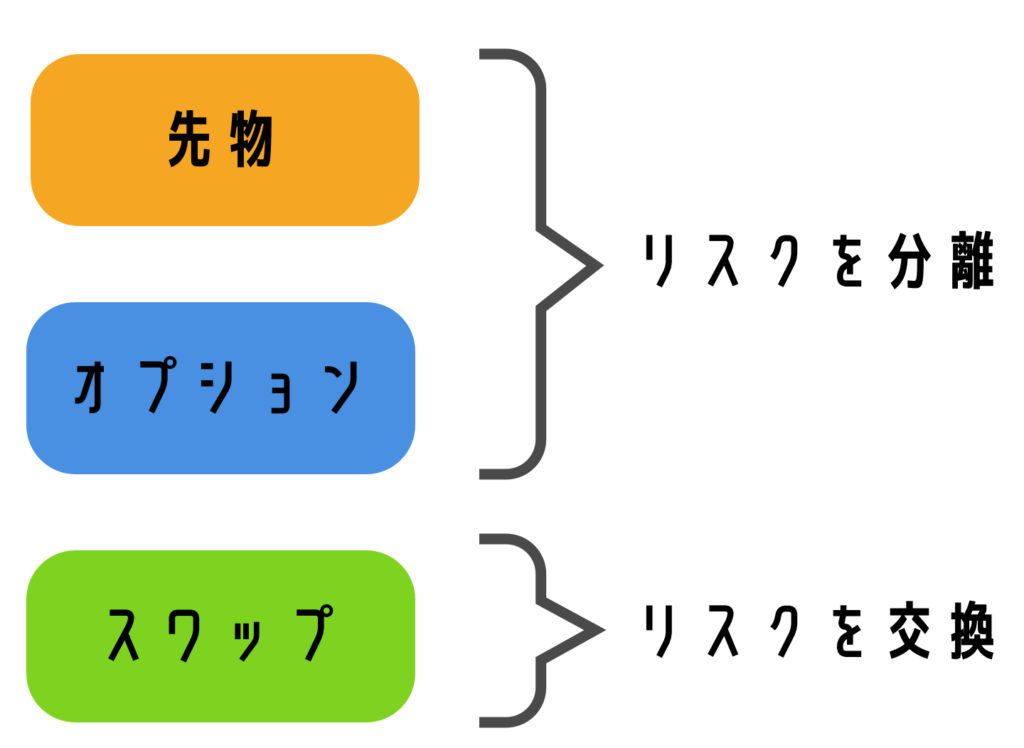
先ほど説明した、先物やオプションはまさに、リスクを分離した商品ですし、スワップは同程度のリスク同士を交換する取引です。

デリバティブ価格理論

ここからは実践的な理論に移っていきます。各種デリバティブが、どのようにリスクとリターンが計算され、そして商品化されていくのかを理解することができます。

あの有名なブラックジョールズモデルについても解説していきます。

現在価格という考え方

金融工学を学び始めて最初につまずくのが現在価格という考え方です。

現在価格とは、「将来受け取れるお金は、現在いくらなのか？」を表したものです。例えば1年後に受け取れる100万円は、現在いくらなのか？を考えます。

将来受け取れる100万円の価値は今も100万円では？と思われる方もいるかもしれませんが異なります。

その理由は、金利を考慮すべきだからです。銀行に100万円を1年間預けていたら金利を受け取れますよね。今の日本の銀行金利は限りなくゼロに近いですが、仮に1%と考えた場合、1年後には101万円になるわけです。

つまり、101万円の現在価格100万円ということになります。

では、1年後の100万円の現在価格はいくらでしょうか？単純に（1+0.01）の逆数を描けるだけです。

となります。簡単ですよね。

この現在価格の考え方によって、将来に渡って受け取る可能性があるあらゆる資産を、全て現在価格に置き換えて比較できるようになりました。これが１つの革命です。

ちなみにこの1/(1+0.01)はディスカウントファクター（Df）と呼ばれています。将来受け取れる金額に対してDfを掛ければ、現在価格を計算できるんだな、と覚えてください。

定式化すると下記の通りです。

オプション理論

オプション理論とは、デリバティブ商品のオプションの設計に用いられている理論です。この理論によって爆発的にデリバティブが増えたと言っても良いでしょう。

オプションの細かな仕組み

先ほども説明しましたがオプションとは、ある時点での「買う権利」と「売る権利」を商品にしています。

例えば下記のオプションについて考えてみます。

現在のソニー株は100円だとします。このオプションを買い、もし1ヶ月後にソニー株が110円になれば、10円の利益を得ることができます。

一方で、もし仮に、ソニー株が90円まで値下がりしたら、100円で買う権利を破棄できます。

損失が出たら権利を破棄できるなんて夢のような取引だと思うかもしれませんが、この「買う権利」には価格がついています。このオプション価格をプレミアムと呼んでいます。値下がりするリスクをオプション価格によって相殺しています。

オプション価格の決定

ではこのオプション価格（プレミアム）をどう決定するのかが金融工学の主要なトピックです。

下記のような状況を考えてみます。

オプションでは値下がりした際に権利を破棄できるため、現在価格より値下がりした場合に、利益がマイナスになることはありません。これらの期待値を計算していくと合計27.5円となることがわかります。

この27.5円がオプション価格になると言いたいところですが、上で現在価格の説明をしましたよね。この値にDf（ディスカウントファクター）を掛けた値がオプション価格となります。

ブラックショールズモデルとは？

では、ここまで理解してある疑問が思い浮かびます。上の表のような株価が●円になる確率が●%なんて予想ができるわけないということです。まさにその通り、そんな予想ができるならみな大金持ちになるはずです。金融工学でも同様で株価は予測できないという前提に立っています。

しかしそのままでは、学問は何の進歩はありません。そこで予想できないという前提のモデルを構築しました。詳しく説明していきます。

よく株価はブラウン運動に例えられます。ブラウン運動とはバケツに張った水に、インクを垂らすと、ゆらゆらと不規則な広がり方を見せると思います。株価も同様で、不規則で上がるか下がるかなんて予想できないと考えます。

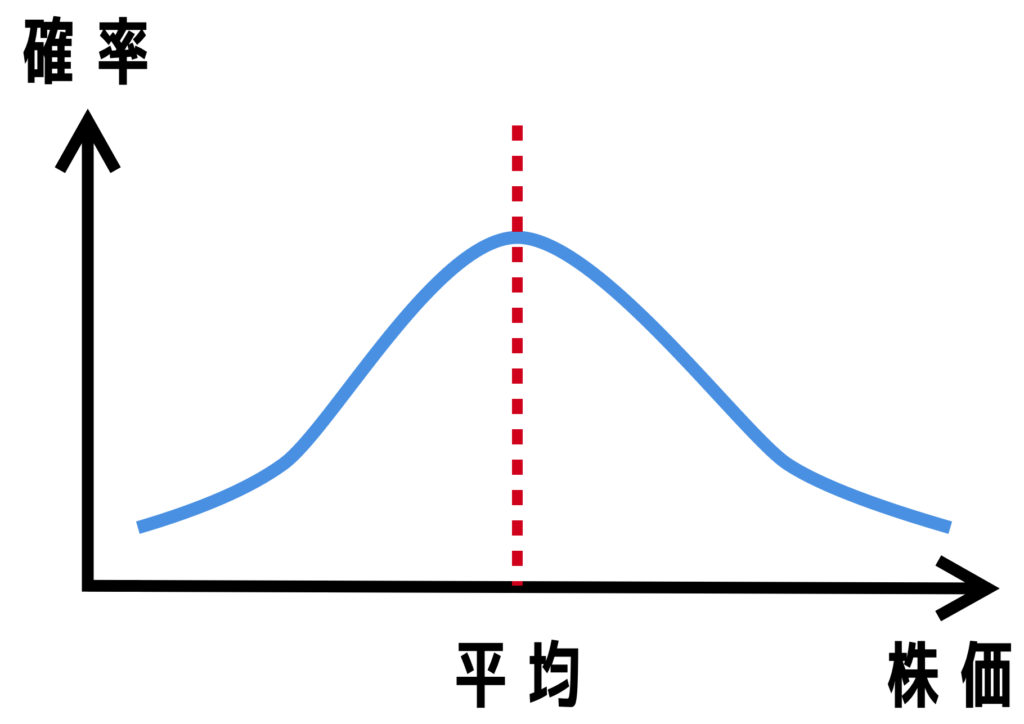
しかし、その不規則な動きもある範囲で収束するということは分かります。つまり、自然現象というのは「ある範囲の中に確率的に収まる」ということは分かっています。これをモデル化したのが正規分布です。

正規分布は、平均から離れれば離れるほど事象が起きにくくなるということを表した表現です。この正規分布を用いてオプション価格を算定します。

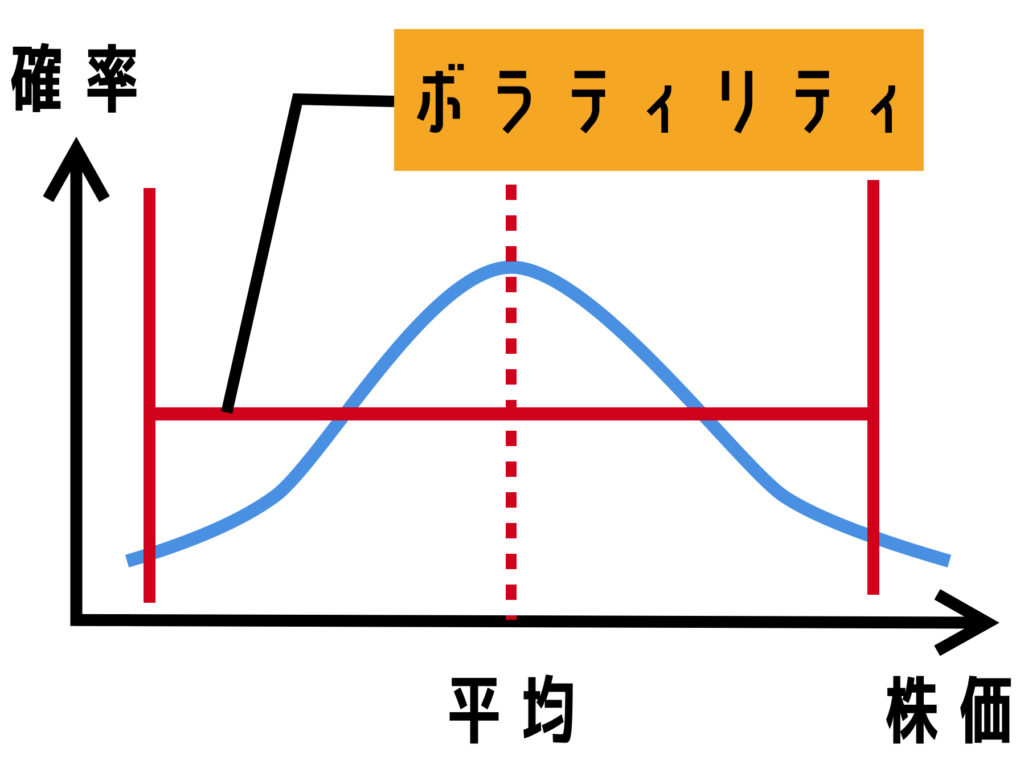
金融工学でも株価はある一定の範囲内に収まるだろうと考えます。これをボラティリティと呼んでおり、ボラティリティが高いとは、その範囲が広いことを意味します。つまり、ボラティリティが高い株は価格が乱高下しやすいという意味です。

このボラティリティは、過去の株価のデータ等を用いて算出します。この範囲に株価は収まるだろうと推定するわけです。

では、ここまできたら、かのブラックショールズモデルの登場です。

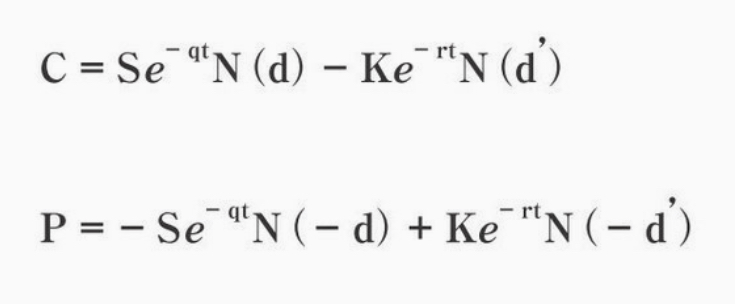
なんのこっちゃ？と多くの人が思われるかと思いますが、このグラフの意味を理解すれば簡単です。

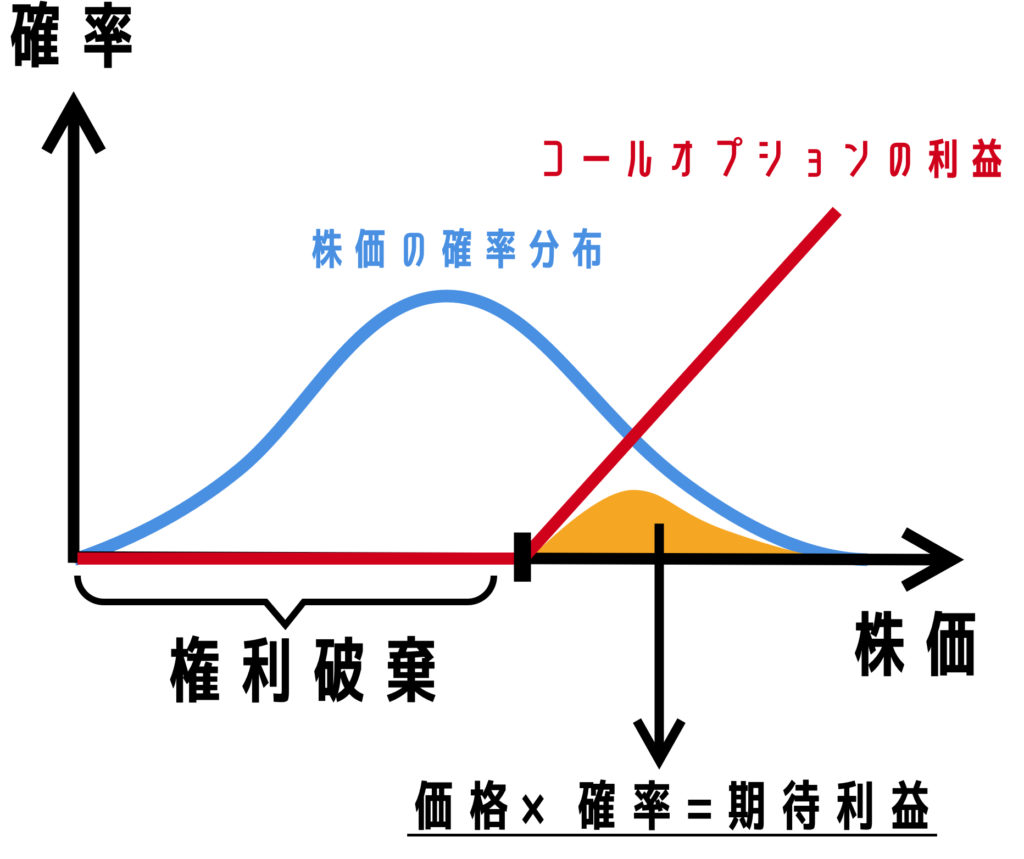
ブラックショールズモデルが意味するのは「株価の確率分布」と「コールオプションの利益」を掛け合わせたオレンジ色の範囲＝期待利益です。つまり期待する利益分をオプション価格とすべきですから、適切なオプション価格（プレミアム）を算出しています。

オプションで得られる利益はある点以上で発生し、右肩上がりとなります。それ以下の場合は権利を放棄するので利益は0となります。それと株価の確率分布の正規分布を重ね合わせます。正規分布の導き方は株価のボラティリティから範囲を割り出します。

金融工学のゆくへ

金融工学はリスクを正確に把握し、リターンの期待値を計算することで、様々なデリバティブを生み出しました。リスクは正確に図られ、リスク同士が交換されるスワップというものも生まれました。デリバティブが生まれたことで金融空間は拡大し、資金の流れが活発になり経済の発展に大きく寄与したことは言うまでもありません。

しかし、注意しなくてはいけないのは、リスクは必ず存在し、そのリスクの受け手が必要だということです。リーマンショックは、リスクが細かく切り刻まれて、様々なデリバティブに組み込まれてリスクが見えない形にされ売り捌かれました。

下記のリンクでリーマンショックについて詳しく解説しています。

リーマンショックをわかりやすく解説 – 原因や影響を10分で簡単に説明 –

我々は金融工学によってリスクを操れるようにはなりましたが、適切に操るかどうかは金融機関次第です。経済を円滑に回すためにも、二度とリーマンショックのようなことを起こしてはいけません。